Метод матричного исчисления
Дана система линейных уравнений
x1-4x2-2x3=-3
3x1+x2+x3=5
-3x1-5x2-6x3=-7
Доказать ее совместимость и решить двумя способами:
Решение:
найдем решение задачи, методом матричного исчисления.
Чтобы записать ее виде матричного уравнения и решить это матричное уравнение, используем правила действия над матрицами.
Для этого введем обозначения:
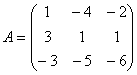 ,
,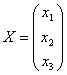 ,
,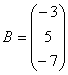
Далее, система записывается в виде следующего уравнения ![]() , откуда следует, что
, откуда следует, что ![]() . Найдем обратную
. Найдем обратную ![]() матрицу для матрицы А. Посчитаем сначала алгебраические дополнения
матрицу для матрицы А. Посчитаем сначала алгебраические дополнения ![]() для элементов
для элементов ![]() матрицы А.
матрицы А.
![]() ,
, ![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
Найдем определитель ![]()
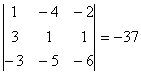 .
.
По формуле для отыскания обратной матрицы имеем
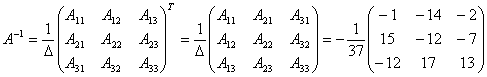
Найдем матрицу строку Х, которая и даст решение системы
х1=53/37; х2=56/37; х3=-30/37
Ответ прост!
Решение задачи методом Гаусса
————————————————————————————————-
Решение задач численные методы. Заказать подобную работу!
————————————————————————————————-
Калькулятор матричного исчисления онлайн
![]()
