Дано уравнение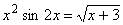 
. Записать вычислительную схему
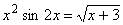. Записать вычислительную схему
a) метода Ньютона,
условие сходимости
Решение:
а) Метод Ньютона:
Вычислительная формула:
.
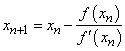Вычислительная формула:
.
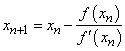Сходится всегда в окрестности корня. Для данного уравнения имеем:
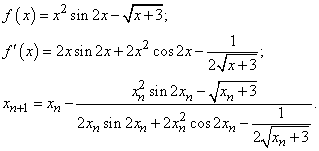
Окончание процесса: когда будет достигнуто требуемое условие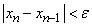 
.
Проиллюстрируем поиск корня на отрезке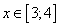 
. Корень на нем есть, так как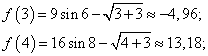 
Итак, в качестве корня на данном интервале можно взять х*=3,260395
b) Метод простой итерации:
Сначала надо уравнение привести к виду, удобному для итерации:
.
Вычислительная формула:
.
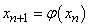Сходится при условии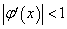
. Для данного уравнения имеем (если корень надо искать вне интервала (-1;1)):
b) Метод простой итерации:
Сначала надо уравнение привести к виду, удобному для итерации:
.Вычислительная формула:
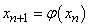. Сходится при условии
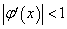. Для данного уравнения имеем (если корень надо искать вне интервала (-1;1)):|
n |
xn |
f(xn) |
f'(xn) |
|
0 |
3 |
-4,96423 |
15,40245 |
|
1 |
3,322301 |
1,388511 |
22,79991 |
|
2 |
3,261401 |
0,022151 |
22,01392 |
|
3 |
3,260395 |
7,98E-06 |
21,99804 |
|
4 |
3,260395 |
1,04E-12 |
21,99803 |
4,179 total views, 1 views today