Исследовать функцию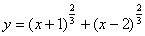 
и построить ее график
I. область определения функции: вся числовая ось, то есть интервал (1+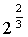
,+∞)
и построить ее графикI. область определения функции: вся числовая ось, то есть интервал (1+
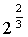,+∞)область значения функции — так как исходная функция состоит из суммы квадратов, то есть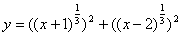 
, имеем интервал [1/2,+∞].
, имеем интервал [1/2,+∞]. Найдем точки пересечения с осями координат:
А) х=0 => y=1+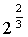≈2,59 -точек пересечения с осью Оy нет
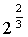≈2,59 -точек пересечения с осью Оy нетБ) у=0 =>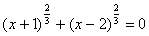 
, 
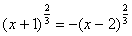, возведем обе части равенства в степень (3), получим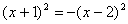 
, , возведем обе части равенства в степень (3), получим 
=> точек пересечения с осью нетФункция не обладает ни свойством четности, ни свойством нечетности. Функция не является периодической.
II. найдем интервалы монотонности функции.
Производная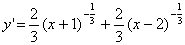
Производная
Интервалы монотонности разделяются точками, в которых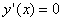 
или не существует. Найдем эти точки:
или не существует. Найдем эти точки: 
=>x=0,5
области определенияРассмотрим интервалы (1+,+∞)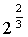
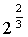,+∞) (1+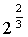,+∞)Здесь 
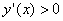функция возрастает
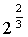,+∞)Здесь функция возрастаетIII. найдем интервалы выпуклости и вогнутости кривой.
=0, если х=1/2области определенияРассмотрим интервал (1+,+∞)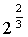
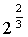,+∞)y« (x) < 0, значит функция выпукла на всей области определения.
IV. осталось рассмотреть поведение функции на бесконечности и установить, имеет ли кривая наклонные асимптоты y=ax+b
Рассмотрим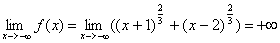
Рассмотрим
Если кривая имеет асимптоту, то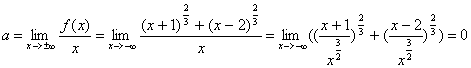 
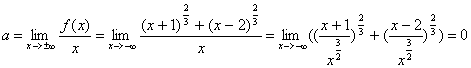
b=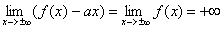
наклонных асимптот у кривой нет
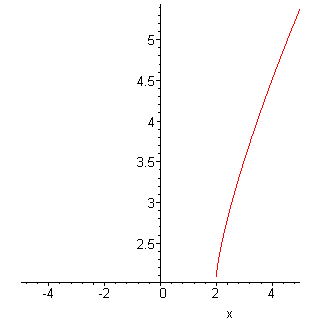
построим график функции:
3,979 total views, 1 views today