Дана функция 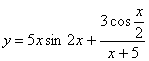 ,
, 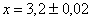 .
.
Найти абсолютную и относительную погрешности вычисления значения y.
Решение:
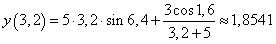 .
.
Абсолютная погрешность:
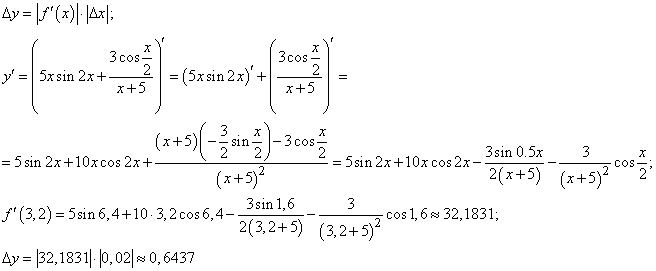
Относительная погрешность: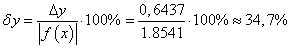 .
.
![]()

В помощь студенту!
готовые задачи на:
Дана функция 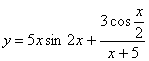 ,
, 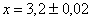 .
.
Найти абсолютную и относительную погрешности вычисления значения y.
Решение:
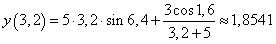 .
.
Абсолютная погрешность:
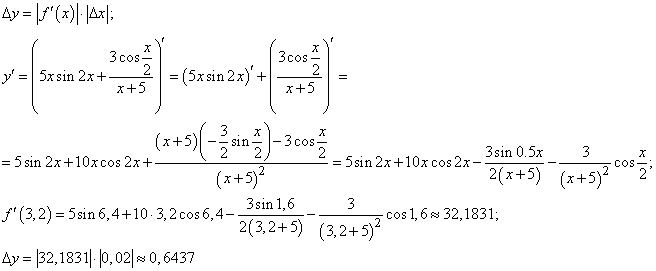
Относительная погрешность: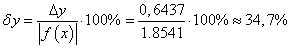 .
.
![]()
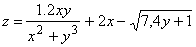 ,
, 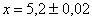 ,
, 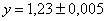 .
.
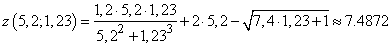 .
.
Абсолютная погрешность:
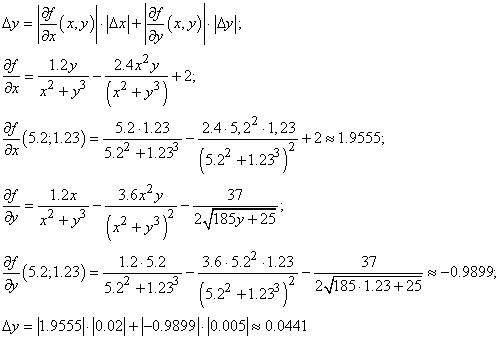
Относительная погрешность:
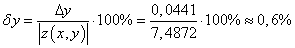 .
.
![]()
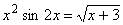 . Записать вычислительную схему
. Записать вычислительную схему
a) метода Ньютона,
условие сходимости
Решение:
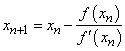 .
.
Сходится всегда в окрестности корня. Для данного уравнения имеем:
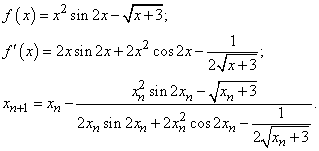
Окончание процесса: когда будет достигнуто
Дана система линейных уравнений
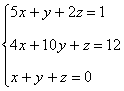 .
.
Записать вычислительную схему метода простой итерации и проверить ее сходимость.
Решение:
Первое уравнение делим на 5; выражаем из получившегося х; второе делим на 10 и выражаем у, из третьего … Читать далее
ЗАДАЧИ:
Дана табличная функция
|
x |
0.1 |
0.4 |
0.7 |
|
y |
5.7 |
8.9 |
9.3 |
Построить для нее интерполяционный полином
а) Ньютона;
б) Лагранжа.
Решение:
а)
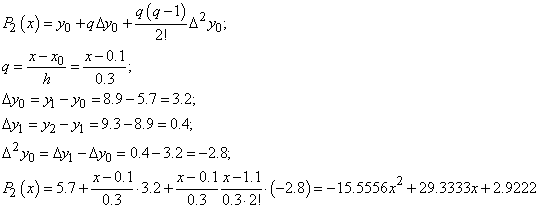
b) 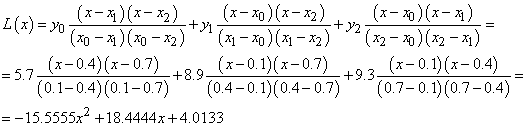
Дан интеграл 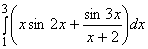 . Для … Читать далее
. Для … Читать далее
Функция y=f(x) задана таблично.
При каком значении x, значения y=40?
x 1,0 1,2 1,4
y 35 55 63
решить задачу обратным интерполированием
решение:
| n | 0 | 1 | 2 |
| х | 1,0 | 1,2 | 1,4 |
| у | 35 | 55 | 63 |
для обратного … Читать далее
| [ Скачать с сервера (26.3Kb) ] | 08.03.2012, 19:56 |
| Задание:
Используя метод Данилевского составить матрицу Фробениуса А= Решение: найдем матрицу Фробениуса, используя вычислительную схему метода Данилевского Выпишем матрицу Фробениуса: Проверим, правильно ли мы нашли матрицу Фробениуса: сумма всех собственных | |
В) … Читать далее
б) … Читать далее
решить … Читать далее