Исследовать
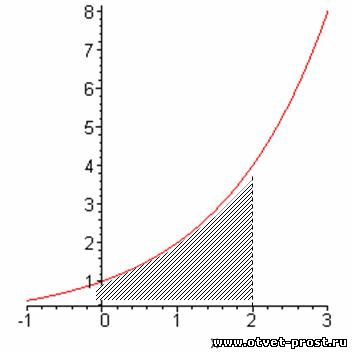
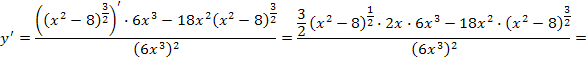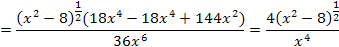… Читать далее площадь фигуры, ограниченной линиями (геометрический смысл производной)
Найдем площадь фигуры , ограниченную линиями: у=2х,х=0,х=2
Сделаем чертеж
слева фигура ограничена прямой х=0, с права х=2, с верху линией у=2х
Sфиг=
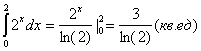
предел х —> ∞ от (1-2х)/(3х-2); lim х —> 0 от (1-cosх)/(5х^2);limх —> ∞ от ((x+3)/(х-2))^x
заказать решение математический анализ, нахождение пределов
Найти пределы:
а)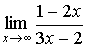 
б)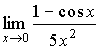 
в)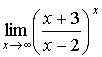 
РЕШЕНИЕ:
а)
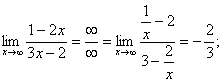
б)
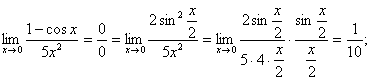
в)
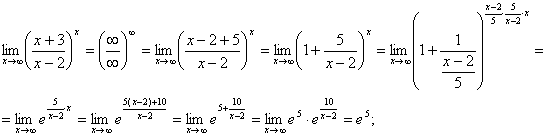
интеграл от смешанных функций
1 интеграл.
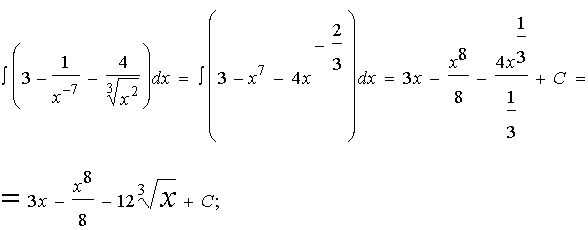
2 интеграл.
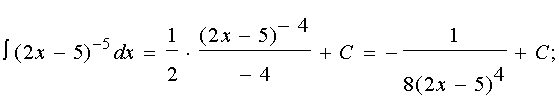
3 интеграл.
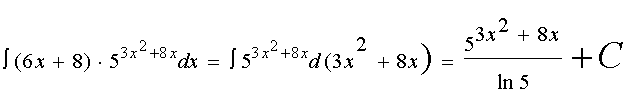
4 интеграл.
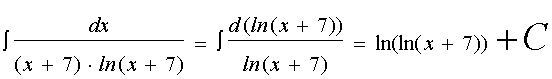
не нашли свой интеграл? пожалуйста не расстраивайтесь, вы всегда можете заказать решение по математике, математическому анализу с помощью формы заказа.
Исследовать функцию и построить график y=(1/2)x^3+3x^2-7
Задание Исследовать функцию и построить график.
.
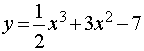Решение:
I. область определения функции: множество действительных чисел R.
область значения функции — множество действительных чисел R.
Найдем точки … Читать далее
для решения краевой задачи применить метод редукции y’’+y=x (**), x є (0,π) y(0)+y’(0)=1,y(π)=0
| [ Скачать с сервера (88.0Kb) ] | 07.11.2013, 17:27 |
| (чтобы увидеть не отображенные картинки, скачайте файл с сервера)
решение будем искать в виде , C – константа, u(x) – ненулевое решение однородного уравнения , функция v(x) – решение неоднородного | |
найти общее решение разностного уравнения у к+1 + у к – 6 у к-1 = к
| [ Скачать с сервера (20.5Kb) ] | 07.11.2013, 17:33 |
| (если отображены не все картинки, скачайте файл с сервера)
найти общее решение разностного уравнения у к+1 + у к – 6 у к-1 = к будем искать решение в виде у | |
Калькулятор для исследования функций
Исследовать функцию онлайн и построить ее график.
С помощью данных калькуляторов можно по шагам провести исследование функции онлайн, и построить график функции онлайн с асимптотами.
Для этого скопируйте исследуемую функцию в каждый калькулятор, как показано в примере, и получите ответ. … Читать далее
Найти площадь фигуры ограниченной кривыми онлайн
Как найти площадь фигуры ограниченной линиями онлайн
Предлагаем Вашему вниманию онлайн калькулятор для нахождения площади фигуры ограниченной кривыми линиями. Калькулятор в автоматическом режиме составляет интеграл, находит границы интегрирования, а также рисует саму фигуру на координатной плоскости. Как частный случай, калькулятор … Читать далее
. 
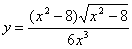