Контрольная работа по логике, вариант 12
Задание 1. Дайте полную логическую характеристику имени (понятия): по объему (единичное, общее, нулевое) и по содержанию (относительное-безотносительное, положительное-отрицательное, абстрактное-конкретное, собирательное-несобирательное):
12. Невиновность.
Решение:
По объему понятие «невиновность» является общим,
По содержанию понятие «невиновность» является безотносительным, отрицательным (отрицает чью-либо вину), несобирательным.
Задание 2. Произведите деление объема имени (понятия) по избранному основанию. Укажите основание деления:
12. Месяц.
Решение:
По времени году, месяц бывает осенним, зимним, весенним или летним.
Основание деления «по времени году».
Задание 3. Изобразите с помощью кругов Эйлера отношение между объемами следующих имен (понятий):
12.Многоэтажное здание, 9-этажный дом, 3-комнатная квартира, комната.
Решение:
Понятия «многоэтажное здание», «9-этажный дом», «3-комнатная квартира», «комната» являются несравнимыми понятиями.
Объем понятия «9-этажный дом» входит в объем понятия «многоэтажное здание», то верно утверждение: Все 9-этажные дома являются многоэтажным зданием.
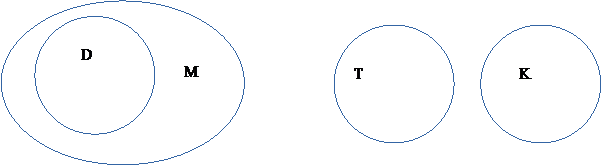
Изобразим с помощью кругов Эйлера отношение между объемами данных понятий:
Пусть М-«многоэтажное здание», D-«9-этажный дом», Т- «3-комнатная квартира», К-«комната».
Задание 4. Укажите, соблюдены ли правила определения в следующих случаях, а если нет, – какие ошибки допущены?
12.Модус – это та часть номинативной конструкции, которая показывает отношение говорящего к пропозиции.
Модус – это та часть номинативной конструкции, которая показывает отношение говорящего к пропозиции.
в данном определении нарушено правило, что определение должно быть ясным. То есть понятие «модус» определяют через неизвестные понятия «номинативной конструкции…», «говорящего к пропозиции…».
Задание 5. Используя логический квадрат, сформулируйте остальные три атрибутивных высказывания. Установите их логическое значение (истинность/ложность), если высказывание, данное в условии, является истинным.
12. Каждое решение, которое вы принимаете, – ошибочно (Э. Далберг).
Решение:
Исходное высказывание «Каждое решение, которое вы принимаете, -ошибочно» является общеутвердительным, перепишем его в виде:
Все решения, которые вы принимаете, являются ошибочными. Пусть оно истинно.
Исходя из отношений логического квадрата, сделаем вывод:
1)Не все решения, которые вы принимаете, не являются ошибочными (будет ложно).
2)Некоторые решения, которые вы принимаете, не являются ошибочными (будет ложью).
3) Некоторые решения, которые вы принимаете, являются ошибочными. (истина)
Задание 6. Произведите непосредственные выводы (превращение (обверсия), обращение (конверсия), противопоставление предикату (частичная контрапозиция):
12. Некоторые люди не терпят лицемерия.
Решение:
Исходное суждение «Некоторые люди не терпят лицемерия»
(О)- частноотрицательное суждение
Схема: Некоторые S не есть Р
Субъект S-«люди», предикат Р-«терпящие лицемерие»
Схема превращения частноотрицательного суждения:
Некоторые S есть не-Р (I-частноутвердительное суждение)
Имеем: Некоторые люди являются теми, кто не терпит лицемерие.
Составить обращение частноотрицательного суждения нельзя.
Схема противопоставления предикату частноотрицательного суждения:
Некоторые не-Р есть S
Имеем: Некоторые нетерпящие лицемерие являются людьми.
Задание 7. Выразите в символической форме структуру рассуждения и табличным способом установите его правильность (является ли оно логическим законом).
12.Если Цезарь не был тираном, то он не заслуживал смерти. А он был тираном. Значит, Цезарь заслуживал смерти.
Решение:
Введем обозначение:
а-«Цезарь был тираном», ¬а – «Цезарь не был тираном»,
b-«Цезарь заслуживал смерти», ¬b- «Цезарь не заслуживал смерти», где «¬» — отрицание.
Выразим рассуждение «Если Цезарь не был тираном, то он не заслуживал смерти. А он был тираном. Значит, Цезарь заслуживал смерти.» в символической форме:
( ((¬а)→(¬b)) /\ а ) → b
Проверим с помощью таблицы истинности правильность полученной формулы:
| a | b | ¬а | ¬b | (¬а)→(¬b) | ((¬а)→(¬b)) /\ а | ( ((¬а)→(¬b)) /\ а ) → b |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
Полученная формула не является тавтологией (1101), следовательно не является логическим законом.
Задание 8. Проанализируйте ПКС, установите (если есть) наличие формальных/содержательных ошибок. Обоснуйте свой ответ, используя общие правила ПКС и правила фигур.
12. Иррационализм опирается на веру, а сциентизм, в свою очередь, отрицает веру, поэтому неудивительно, что иррационализм не суть сциентизм.
Решение:
Представим в общем виде:
Большая посылка: Любой сциентизм (Р+) не является опорой на веру (М+)
Меньшая посылка: Любой иррационализм (S+) является опорой на веру (М-)
—————————————————————————————————-
Заключение: Любой иррационализм (S+) не суть сциентизм (Р+)
Имеем:
(Е): Все Р не суть М
(А): Все S суть М
—————————
(Е): Все S не суть Р
Проверим правила категорического силлогизма:
1)В силлогизме три термина. (выполнено, имеем три термина S-«иррационализм», Р-«сциентизм», М-«опора на веру»)
2)средний термин должен быть распределен, хотя бы в одной из посылок (выполнено, средний термин М распределен в большой посылке)
3)Термин, не распределенный в посылке, не может быть распределен в выводе (выполнено)
4)в силлогизме не должно быть двух отрицательных посылок (выполнено, только большая посылка является отрицательной)
5)в силлогизме не должно быть двух частных посылок (выполнено, обе посылки являются общими)
6)если одна из посылок отрицательная, то и вывод должен быть отрицательным (выполнено)
7)если одна из посылок частная, то и вывод должен быть частным (не относится к нашему случаю)
Имеем дело со второй фигурой категорического силлогизма:
Р-М
S-М
Проверим правила 2 фигуры:
1)большая посылка должна быть общим суждением (выполнено)
2)одна из посылок должна быть отрицательной (выполнено)
Все правила соблюдены, значит вывод следует с необходимостью.
Задание 9. Восстановите знтимему до полного силлогизма и установите ее правильность.
12.На Луне нет жизни, следовательно, там нет атмосферы.
Решение:
На Луне нет жизни, следовательно, там нет атмосферы.
Потому как присутствуют слова «следовательно, там …» значит есть вывод, а отсутствует посылка. Выясним, какая меньшая посылка или большая.
Большая посылка: —
Меньшая посылка: На луне (S+) нет жизни (М+)
——————————————————————
Вывод: На луне (S+) нет атмосферы (Р-)
Видно, что пропущена большая посылка. Предположим, что имеем дело с 1 фигурой категорического силлогизма
М—Р
S—M
Согласно правилам 1 фигуры, общая посылка, должна быть общим суждением (A,E)
(А): Любое отсутствие жизни (М+) это отсутствие атмосферы(Р-)
(А): На луне (S+) нет жизни (М-)
——————————————————————
(А): На луне (S+) нет атмосферы (Р-)
Имеем достоверный вывод.
Задание 10 . Произведите обобщение и ограничение объема имени (наличие двух этапов ограничения / обобщения – необходимое условие выполнения задания).
12.Обвинительный приговор.
Решение:
Обобщение понятия «обвинительный приговор»:
Обвинительный приговор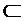 процессуальный акт правосудия
процессуальный акт правосудия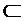 акт правосудия
акт правосудия
Ограничение понятия «обвинительный приговор»:
Обвинительный приговор 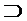 Обвинительный приговор по делу
Обвинительный приговор по делу 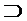 обвинительный приговор по делу о краже
обвинительный приговор по делу о краже
![]()
