1.Для формулы: А&(B—>A)—>┐A , записать двойственную ей и отрицание. Сформулировать принцип двойственности.
Решение:
учитывая силу «связывания» логических операций построим формулу, реализующую функцию, двойственную к
f(A,B)= А&(B—>A)—>┐A
![]()
Отрицание исходной формулы:
![]()
Сформулируем принцип двойственности:
Функция f*(x1, …, xn) называется двойственной к функции f(x1, …, xn), если f*(x1, …, xn) = (1, …, n). функций заменить на двойственные, 0 на 1, 1 на 0.
2.Записать формулу A—>B&C в СДНФ и СКНФ, используя таблицу истинности
Решение:
Построим таблицу истинности для трех переменных:
| А | В | С | В&С | A—>B&C |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Построим СДНФ формулы :
1.выпишем наборы, где функция принимает значения, равные единице
000,001,010,011,111
2.составим конъюнкции этих переменных
![]()
3.составим дизъюнкцию полученных конъюнкций, это и будет СДНФ
![]()
Построим СКНФ формулы:
1.выпишем наборы, где функция равна нулю
100,101,110
2.составим дизъюнкции этих переменных(учтем, что если 1, то отрицание переменной записываем; если 0, то записывается сама переменная)
![]() 3.составим конъюнкцию полученных дизъюнктов, это и будет СКНФ
3.составим конъюнкцию полученных дизъюнктов, это и будет СКНФ
![]()
3. Записать полином Жегалкина для формулы: А&(B—>A)—>┐A
Решение:
Построим таблицу истинности для формулы А&(B—>A)—>┐A
| А | В | B—>A | A&(B—>A) | ┐A | А&(B—>A)—>┐A |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Общий вид полинома Жегалкина
![]()
Методом треугольника Паскаля найдем полином Жегалкина:
строим вспомогательную таблицу, в которой первый столбец совпадает со столбцом значений функции в таблице истинности
ячейки в каждом последующем столбце получаем путем суммирования по модулю 2 двух ячеек предыдущего столбца – стоящей в той же строке и строкой ниже
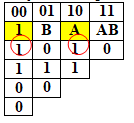
Получили полином Жегалкина для формулы А&(B—>A)—>┐A
равен P=1![]() А
А
4.определить принадлежность функций системы пяти замкнутым классам. Проверить выполнение условий теоремы Поста для системы БФ: f1=x—>y, f2=![]() , f3=xy
, f3=xy
Решение:
Построим таблицу истинности для функций данной системы:
| х | у | f1=x—>y | f2= |
f3=xy |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
1.Так как f1,f2, не сохраняют ноль, f3 сохраняет ноль, то система {f1,f2,f3} будет сохраняющей ноль
2.Так как f2 не сохраняет единицу, а f1,f3 сохраняют единицу, то система{f1,f2,f3}будет сохраняющей единицу
3.Так как f2 самодвойственная функция (на противоположных наборах она принимает противоположные значения), то система{f1,f2,f3}будет принадлежать классу самодвойственных функций
4.так как f2 и f3 монотонные функции, то система{f1,f2,f3}будет принадлежать классу монотонных функций
5.построим полином Жегалкина для каждой из трех функций системы, чтобы выяснить являются ли он линейными функциями:
| Для f1, полином Жегалкина имеет вид: P=1 Значит функция f1 не линейная 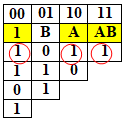 |
Для f2, полином Жегалкина имеет вид: P=1 Значит функция f2 линейная функция 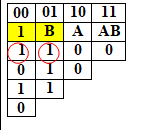 |
Для f3, полином Жегалкина имеет вид: P=АВ Значит функция f3 не линейная функция 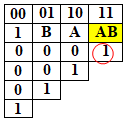 |
Отсюда имеем, что система{f1,f2,f3}будет принадлежать классу линейных функций
5.минимизировать БФ: f(x,y,z,t)=∑(2,3,0,8,9,12,13,14,15)
Решение:
Составим таблицу истинности для данной функции от четырех переменных:
| Номер k | x | y | z | t | f(x,y,z,t) |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 |
Дли минимизации используем, метод Диаграмм Вейча:
Метод позволяет быстро получать минимальные ДНФ булевой функции f небольшого числа переменных. В основе метода лежит задание булевых функций диаграммами некоторого специального вида, получившими название диаграмм Вейча.
Перерисуем таблицу истинности в двухмерный вид:
|
z t
х у |
0
0 |
0
1 |
1
1 |
1
0 |
| 0 0 | 0000 | 0001 | 0011 | 0010 |
| 0 1 | 0100 | 0101 | 0111 | 0110 |
| 1 1 | 1100 | 1101 | 1111 | 1110 |
| 1 0 | 1000 | 1001 | 1011 | 1010 |
Подставив значения функции, получим
|
z t
х y |
0
0 |
0
1 |
1
1 |
1
0 |
| 0 0 | 1 | 1 | 1 | |
| 0 1 | ||||
| 1 1 | 1 | 1 | 1 | 1 |
| 1 0 | 1 | 1 |
Минимизируем в соответствии с правилами:
Сама минимизация производится по следующим правилам (на примере ДНФ):
- Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала 2n (n целое число = 0…) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули;
- Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
- Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну;
- Область должна быть как можно больше, а количество областей как можно меньше;
- Области могут пересекаться;
- Возможно несколько вариантов покрытия.
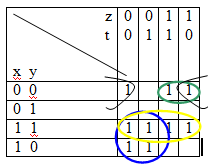
Получили 4 области,
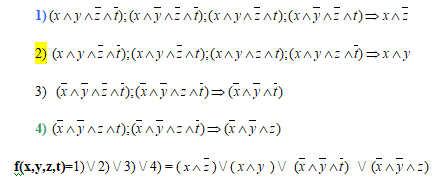
6.Выяснить, какую БФ реализует схема.
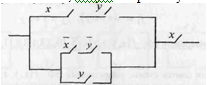
Представить в виде схемы из ФЭ, оптимизировав по их числу
Решение:
Запишем, какую булеву функцию реализует данная схема:
![]()
Если преобразовать формулу, то получим
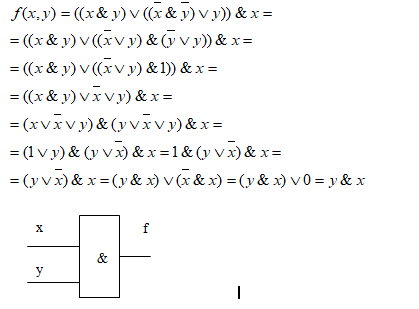
![]()
